堆排序 | 十大排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列； 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

思路

创建一个堆 H[0……n-1]；

把堆首（最大值）和堆尾互换；

把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；

重复步骤 2，直到堆的尺寸为 1。

图解

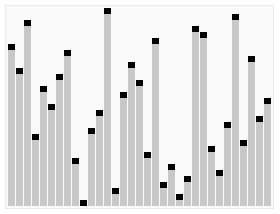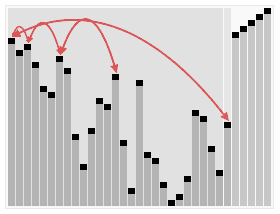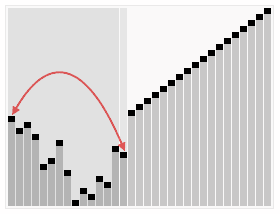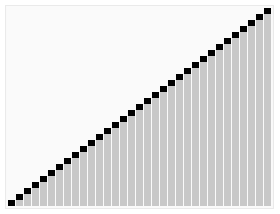
代码

/// <summary>
/// 堆排序
/// </summary>
/// <param name="arr">待排序数组</param>
static void HeapSort(int[] arr)
{
    int vCount = arr.Length;
    int[] tempKey = new int[vCount + 1];
    // 元素索引从1开始
    for (int i = 0; i < vCount; i++)
    {
        tempKey[i + 1] = arr[i];
    }
    // 初始数据建堆（从含最后一个结点的子树开始构建，依次向前，形成整个二叉堆）
    for (int i = vCount / 2; i >= 1; i--)
    {
        Restore(tempKey, i, vCount);
    }
    // 不断输出堆顶元素、重构堆，进行排序
    for (int i = vCount; i > 1; i--)
    {
        int temp = tempKey[i];
        tempKey[i] = tempKey[1];
        tempKey[1] = temp;
        Restore(tempKey, 1, i - 1);
    }
    //排序结果
    for (int i = 0; i < vCount; i++)
    {
        arr[i] = tempKey[i + 1];
    }
}
/// <summary>
/// 二叉堆的重构（针对于已构建好的二叉堆首尾互换之后的重构）
/// </summary>
/// <param name="arr"></param>
/// <param name="rootNode">根结点j</param>
/// <param name="nodeCount">结点数</param>
static void Restore(int[] arr, int rootNode, int nodeCount)
{
    while (rootNode <= nodeCount / 2) // 保证根结点有子树
    {
        //找出左右儿子的最大值
        int m = (2 * rootNode + 1 <= nodeCount && arr[2 * rootNode + 1] > arr[2 * rootNode]) ? 2 * rootNode + 1 : 2 * rootNode;
        if (arr[m] > arr[rootNode])
        {
            int temp = arr[m];
            arr[m] = arr[rootNode];
            arr[rootNode] = temp;
            rootNode = m;
        }
        else
        {
            break;
        }
    }
}